Luminescências

Pitágoras não só se satisfez com a generalização da propriedade a que chegou, como também se preocupou com a sua demonstração, ou seja, em provar que essa regra se aplicava a todos os triângulos rectângulos. Só depois de demonstrada a propriedade seria promovida a teorema. Teorema este que era uma propriedade que para ser aceite como verdadeira, necessita de ser demonstrada. Pitágoras considerou um triângulo rectângulo cujos lados mediam, numa dada unidade, a e b, e a hipotenusa, c.




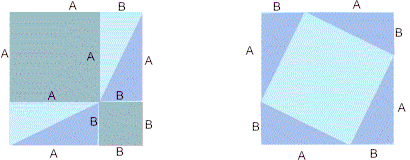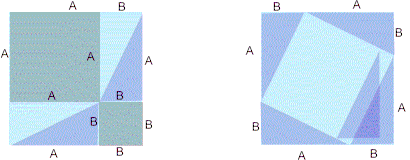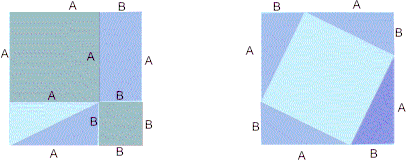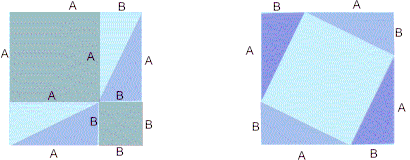
Cada figura é um quadrado de lado a + b. A figura 1 foi subdividida em quatro triângulos iguais ao inicial e num quadrado de lados iguais á hipotenusa c .

A figura 2 também contêm quatro triângulos iguais ao inicial.

Pode-se concluir que se temos dois quadrados iguais e ambos contêm quatro triângulos iguais ao inicial, então o que resta num quadrado , noutro tem de ser igual. Pitágoras concluiu que: a^2 + b^2 = c^2

Por volta de 4000 a.C. os Egiptos já utilizavam o método de traçar ângulos rectos, utilizando uma corda onde eram dados 13 nós de forma a que o espaço entre eles fosse igual, isto é, a corda media 12 unidades, sendo cada unidade o espaço entre dois nós consecutivos.

Em seguida, três pessoas seguravam a corda, unindo os dois extremos e a fim de construírem um triângulo cujos lados medissem 3, 4 e 5 unidades. Tinham assim a certeza de que o ângulo b era recto. Esta igualdade verifica-se para qualquer triângulo rectângulo e sua generalização ficou conhecida pelo teorema de Pitágoras.